이번 주제는 분할적 군집화의 프로토타입 기반 기법 중 K-중심군집(K-centroid Clustering)이다.
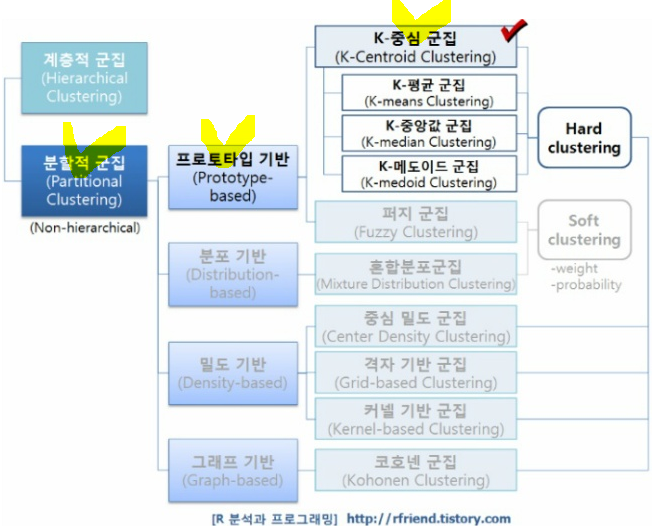
K-중심군집(K-centroid Clustering) 이란?
프로토타입 기반 군집화(Prototype-based Clustering)는 미리 정해놓은 각 군집의 프로토타입에
각 객체가 얼마나 유사한가를 가지고 군집을 형성하는 기법이다.
K-중심군집에서는
연속형 데이터의 경우 평균(mean)이나 중앙값(median)을 그 군집의 프로토 타입으로 하며,
이산형 데이터의 경우 최빈값(mode)이나 메도이드(medoid)로 해당 군집을 가장 잘 나타내는 측도를 정해
프로토타입으로 정하게 된다.
'평균(Mean)'을 쓰는 K-means Clustering, '중앙값(Median)'을 쓰는 K-median Clustering,
'메도이드(Medoid)'를 쓰는 K-medoid Clustering 등으로 세분화되며,
이들을 모두 묶어서 K-중심군집(K-centroid Clustering)이라고 한다.
여기서 K 는 군집의 수(number of clusters)를 나타내는 모수(parameter)로서,
분석가가 사정에 정의해주어야하며,
K를 미리 지정해주어야 하는 군집분석 기법으로는 이번 주제인 K-중심군집(K-centroid Clustering) 외에
퍼지군집(Fuzzy Clustering), 혼합분포 군집(Mixture Distribution Clustering) 등이 있다.
K-중심군집(K-centroid Clustering) 의 원리
1. 군집 내 응집도 최대화(maximizing cohesion within cluster)
: 군집 내 중심(centroid)과 해당 군집의 각 객체 간 거리의 합 최소화 하는것
2. 군집 간 분리도 최대화(maxizing separation between clusters)
: 각 군집의 중심(centroid) 間 거리 합 최대화하는것
의 두 가지 목적함수를 만족하는 솔루션을 찾는것이다.
즉, 군집분석은 결국 위의 두 목적함수에 대한
최적화 (optimization of global objective function) 문제임을 알 수 있다.
복잡도(complexity)를 살펴보면, 군집의 수가 k, 차원의 수가 d, 객체의 수가 n 일 때

이다. (*출처)
기본적으로 객체의 수(n)가 많을 수록 시간이 오래걸리며,
특히 변수의 수(d)와 군집의 수(k)가 늘어날 수록 지수적으로 계산 시간이 증가함을 알 수 있다.
따라서 허접한 변수들 몽땅 때려넣고 군집화하라고 컴퓨터한테 일 시킬 것이 아니라,
똘똘하고 핵심적인 변수를 선별해서 차원을 줄인 후에 군집분석을 실행하는 것이
연산시간을 줄이는 측면에서나, 잘 군집화가 되도록 하는 측면에서나 중요하다.
'통계 > 통계지식' 카테고리의 다른 글
| [통계] p-value란 무엇인가? 짧고 굵은 기본개념! (0) | 2021.01.04 |
|---|---|
| [모델성능 평가지표] (1) 회귀모델 (0) | 2020.11.05 |
| [군집분석] 군집분석이란? (군집분석 종류, 계층적군집화, 분할적군집화) (0) | 2020.11.04 |
| [통계적 검정] 통계적 검정이란? (0) | 2020.11.04 |
| [통계] 통계란? (개념, 표본추출방법, 명목척도,순서척도,구간척도,비율척도) (0) | 2020.11.03 |